【やさしい電磁気学】E-H対応とE-B対応の等価性

HOME ＞電磁気学＞静磁場＞ E-H対応とE-B対応の等価性

【前ページ】【次ページ】

Contents

本ページでは…
前ページまで…
内容

本ページでは…

本ページでは、E-H対応とE-B対応は等価であることを明らかにする。

前ページまで…

前ページでは、E-B対応における静磁場の理論で登場した各単語について説明をまとめた。

内容

E-H対応とE-B対応の等価性

磁気現象を磁荷によって説明するE-H対応において、構成方程式は

\begin{align*}\boldsymbol H=\frac{1}{\mu_0}(\boldsymbol B-\boldsymbol P_{\text m})\tag{1}\end{align*}

であり、磁束密度\(\boldsymbol B\)が源場、磁場\(\boldsymbol H\)が力場である(以前のページを参照)。磁束密度\(\boldsymbol B\)が磁性体を下から上に貫くときを考えると、磁性体下部には負の分極磁荷\(-Q_{\text{mb}}\)、磁性体上部には正の分極磁荷\(+Q_{\text{mb}}\)が現れるため、磁気分極にマイナスを掛けた量\(-\boldsymbol P_{\text m}\)は磁性体内部では上から下に、磁性体外部では正の分極磁荷からグルりと磁性体を回り込んで負の分極磁荷に向かうベクトル場となる(以前のページを参照)。

\begin{align*}-\int_S\boldsymbol P_{\text m}\cdot d\boldsymbol S=Q_{\text{mb}}\tag{2}\end{align*}

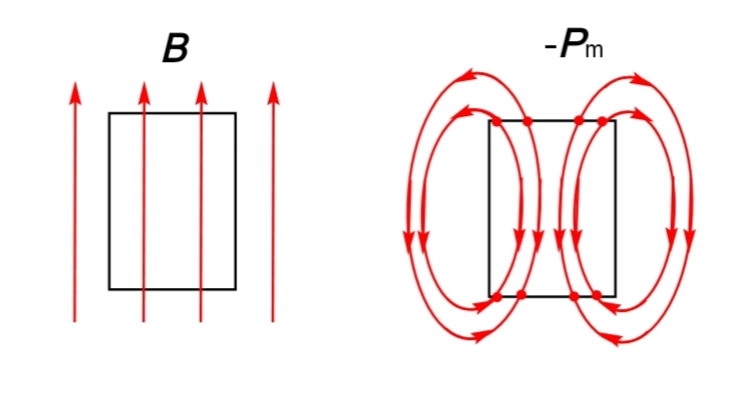
つまり、磁性体内部と磁性体外部の横空間の磁場\(\boldsymbol H\)は弱められ、磁性体外部の上方＆下方空間の磁場\(\boldsymbol H\)は強められる。そして、磁束密度\(\boldsymbol B\)は磁性体外部･内部で連続だが、磁気分極\(\boldsymbol P_{\text m}\)と磁場\(\boldsymbol H\)は不連続となる。

一方、磁気現象を電流によって説明するE-B対応において、構成方程式は

\begin{align*}\boldsymbol B=\mu_0(\boldsymbol H+\boldsymbol M)\tag{3}\end{align*}

であり、磁場\(\boldsymbol H\)が源場、磁束密度\(\boldsymbol B\)が力場である(以前のページを参照)。磁場\(\boldsymbol H\)が磁性体を下から上に貫くときを考えると、磁性体の側面には束縛電流\(I_{\text b}\)が現れるため、磁化\(\boldsymbol M\)は磁性体内部では下から上に、磁性体外部ではグルりと磁性体を回り込んで上から下に向かうループ状のベクトル場となる(以前のページを参照)。

\begin{align*}\int_C\boldsymbol M\cdot d\boldsymbol l=I_{\text b}\tag{4}\end{align*}

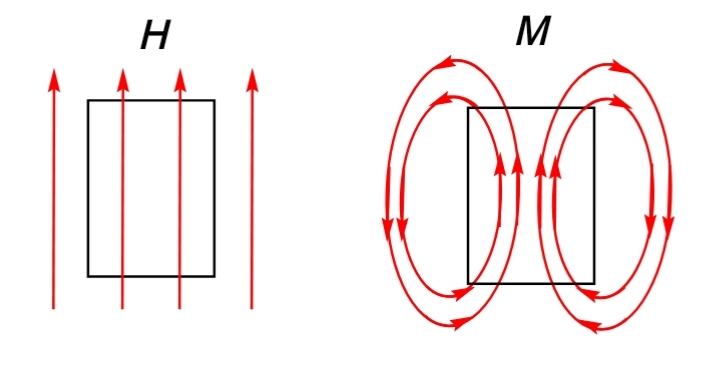
つまり、磁性体外部の横空間の磁束密度\(\boldsymbol B\)は弱められ、磁性体内部および磁性体外部の上方＆下方空間の磁束密度\(\boldsymbol B\)は強められる。そして、磁場\(\boldsymbol H\)と磁化\(\boldsymbol M\)と磁束密度\(\boldsymbol B\)は連続となる。

このように、どちらの対応をとるかによって源場と力場は反対になり、連続性も変わるため、E-H対応とE-B対応は等価でないと思うかもしれない。しかし、E-H対応とE-B対応は等価であり、このことを磁性体が存在しない場合と磁性体が存在する場合に分けて確認していく。

磁性体が存在しないとき

E-H対応において、磁性体が存在しないとき、源場の磁束密度\(\boldsymbol B\)と力場の磁場\(\boldsymbol H\)との関係は真空の透磁率\(\mu_0\)を用いて

\begin{align*}\boldsymbol H=\frac{1}{\mu_0}\boldsymbol B\tag{5}\end{align*}

となる(以前のページを参照)。一方、E-B対応において、磁性体が存在しないとき、源場の磁場\(\boldsymbol H\)と力場の磁束密度\(\boldsymbol B\)との関係は真空の透磁率\(\mu_0\)を用いて

\begin{align*}\boldsymbol B=\mu_0\boldsymbol H\tag{6}\end{align*}

となる(以前のページを参照)。

式(5)と式(6)を見比べるとどちらも同じ式であるため、磁性体が存在しないとき、E-H対応とE-B対応は等価である。

磁性体が存在するとき

磁性体内部

磁気分極\(\boldsymbol P_{\text m}\)は単位体積あたりの磁気双極子モーメントの総和

\begin{align*}\boldsymbol P_{\text m}=\frac{\sum_{i=1}^n\boldsymbol p_{\text m,i}}{\Delta V}\tag{7}\end{align*}

であり(以前のページを参照)、磁化\(\boldsymbol M\)は単位体積あたりの磁気モーメントの総和

\begin{align*}\boldsymbol M=\frac{\sum_{i=1}^n\boldsymbol m_i}{\Delta V}\tag{8}\end{align*}

であった(以前のページを参照)。磁気双極子モーメント\(\boldsymbol p_{\text m}\)と磁気モーメント\(\boldsymbol m\)との間には次の関係

\begin{align*}\boldsymbol p_{\text m}=\mu_0\boldsymbol m\tag{10}\end{align*}

が成り立つため、磁気分極\(\boldsymbol P_{\text m}\)と磁化\(\boldsymbol M\)の間には次の関係

\begin{align*}\boldsymbol P_{\text m}=\mu_0\boldsymbol M\tag{10}\end{align*}

が成り立つ。ここで、式(7)と式(8)は単位体積に含まれる磁気双極子モーメントまたは磁気モーメントの総和であるため磁性体内部でしか成り立たず、磁性体内部でのみ式(10)は成り立ち、この式(10)が成り立てば式(1)と式(3)は等しくなる。つまり、磁性体内部では磁束密度\(\boldsymbol B\)と磁場\(\boldsymbol H\)はE-H対応でもE-B対応でも同じ値になることが分かる。

磁性体外部

磁性体外部では式(10)は成り立たないため、磁場\(\boldsymbol B\)と磁束密度\(\boldsymbol H\)はE-H対応とE-B対応で同じ値をとらない。

具体的には、E-H対応では磁性体外部の上方＆下方空間では磁場\(\boldsymbol H\)は\(\boldsymbol B/\mu_0\)より強められ、磁性体外部の横空間では磁場\(\boldsymbol H\)は\(\boldsymbol B/\mu_0\)より弱められる一方、E-B対応では磁性体外部の上方＆下方空間では磁束密度\(\boldsymbol B\)は\(\mu_0\boldsymbol H\)より強められ、磁性体外部の横空間では磁束密度\(\boldsymbol B\)は\(\mu_0\boldsymbol H\)より弱められる。つまり、E-H対応とE-B対応で\(\boldsymbol H\)と\(\boldsymbol B/\mu_0\)(または\(\boldsymbol B\)と\(\mu_0\boldsymbol H\))の大小関係は真逆になる。

しかし、E-H対応では常に力場は磁場\(\boldsymbol H\)であり、E-B対応では常に力場は磁束密度\(\boldsymbol B\)であるから、E-H対応またはE-B対応のどちらかを一貫して用いていれば大小関係がE-H対応 or E-B対応によって異なっていても問題ない。(｢源場を考えるときはE-H対応で、力場を考えるときはE-B対応を用いる｣などのように二つの対応を混在させなければ問題ないということである。)

磁性体内部の磁束密度

磁性体内部の磁束密度\(\boldsymbol B\)を測定したいとき、磁性体内部に磁場方向を軸とした薄くて広い円盤状空洞を作り、その空洞内で測定すればよい。

E-H対応で考えると、薄くて広い円盤状空洞の両面に分極磁荷が生じ、磁性体表面の分極磁荷が作る磁気分極\(\boldsymbol P_{\text m}\)を打ち消すため、源場である磁束密度\(\boldsymbol B\)が観測される。

注釈

広い平面である磁性体の表面に分極磁荷が一様に現れるとき、各分極磁荷から生じる磁気力線は平面に対して垂直方向以外の成分はそれぞれ打ち消し合って、平面に対して垂直方向の成分しか残らない。

また、薄くて広い円盤状空洞の両面に分極磁荷が一様に現れるとき、各分極磁荷から生じる磁気力線は平面に対して垂直方向以外の成分はそれぞれ打ち消し合って、平面に対して垂直方向の成分しか残らない。

つまり、｢磁性体が作る磁気分極｣や｢薄くて広い円盤状空洞が作る磁気分極｣は位置によらず同じ値となる。そして、｢磁性体が作る磁気分極｣と｢薄くて広い円盤状空洞が作る磁気分極｣で正磁荷･負磁荷の配置が逆のため、磁気分極は互いに打ち消し合う。

電磁気学ではよく｢一様な磁束密度を磁性体に掛ける｣と言うが、一様な磁束密度とはこのように十分広い平面に磁荷を並べることによって作られる。

一方、E-B対応で考えると、薄くて広い円盤状空洞の側面は小さいため生じる束縛電流は無視でき、力場である磁束密度\(\boldsymbol B\)が観測される。

磁性体内部の磁場

磁性体内部の磁場\(\boldsymbol H\)を測定したいとき、磁性体内部に磁場方向に沿って細長い円筒状空洞を作り、その空洞内で測定すれば良い。

E-H対応で考えると、細長い円筒状空洞の両面は小さいため生じる分極磁荷は無視でき、力場である磁場\(\boldsymbol H\)が観測される。

一方、E-B対応で考えると、細長い円筒状空洞の側面に束縛電流が生じ、磁性体表面の束縛電流が作る磁化\(\boldsymbol M\)を打ち消すため、源場である磁場\(\boldsymbol H\)が観測される。

注釈

長い円筒状の磁性体の側面に束縛電流が一様に現れるとき、各束縛電流から生じる磁束は側面方向以外の成分はそれぞれ打ち消し合って、側面方向の成分しか残らない。

また、細長い円筒状空洞の側面に束縛電流が一様に現れるとき、各束縛電流から生じる磁束は側面方向以外の成分はそれぞれ打ち消し合って、側面方向の成分しか残らない。

つまり、｢磁性体が作る磁化｣や｢細長い円筒状空洞が作る磁化｣は位置によらず同じ値となる。そして、｢磁性体が作る磁化｣と｢細長い円筒状空洞が作る磁化｣で束縛電流の流れの向きが逆のため、磁化は互いに打ち消し合う。

電磁気学ではよく｢一様な磁場を磁性体に掛ける｣と言うが、一様な磁場とはこのように十分長い円筒状に環状電流を並べる(ソレノイドを作る)ことによって作られる。

源場と力場を入れ替わる理由

E-H対応において、源場である磁束密度\(\boldsymbol B\)の単位は\(\text{Wb}\cdot\text m^{-2}\)であり、力場である磁場\(\boldsymbol H\)の単位は\(\text N\cdot \text{Wb}^{-1}\)であった。一方、E-B対応において、力場である磁束密度\(\boldsymbol B\)の単位は\(\text N\cdot\text A^{-1}\text m^{-1}\)であり、源場である磁場\(\boldsymbol H\)の単位は\(\text A\cdot\text m^{-1}\)であった。

どちらの対応でも単位は等しいため、単位ウェーバ\(\text {Wb}\)と単位アンペア\(\text A\)の間には次の関係

\begin{align*}\text {Wb}=\text {N}\ \text m\cdot\text A^{-1}\tag{11}\end{align*}

が成り立つ。単位ボルト\(\text V\)にアンペア\(\text A\)を掛けると単位ワット\(\text W\)になるため、次の関係式

\begin{align*}\text V\ \text A&=\text W\\&=\text J\cdot \text s^{-1}\\&=\text N\ \text {m}\cdot\text s^{-1}\\\rightarrow\text A&=\text {N}\ \text m\cdot\text V^{-1}\ \text {s}^{-1}\tag{12}\end{align*}

が成り立ち、式(11)に代入すると

\begin{align*}\text {Wb}=\text {V}\ \text s\tag{13}\end{align*}

となる。一方、電流\(I\)は1秒あたりに通過するクーロン量\(C\)であるため、電流\(I\)の単位のアンペア\(\text A\)は

\begin{align*}\text A=\text C\ \text s^{-1}\tag{14}\end{align*}

となり、次のように変形できる。

\begin{align*}\text C=\text {A}\ \text s\tag{15}\end{align*}

式(13)と式(15)を見比べると磁荷と電荷に対称性が見られ、式(13)より1秒あたりの磁荷(または磁束)の変化が電位であり、式(15)より1秒あたりの電荷(または電束)の変化が電流であることがわかる。つまり、E-H対応とE-B対応で源場と力場を入れ替える理由はこの対称性を明らかにするためである。

また、量子論にはなるが、単位ウェーバ\(\text {Wb}\)と単位クーロン\(\text C\)の積は

\begin{align*}\text {Wb}\ \text{C}&=\text V\ \text A\ \text s^2\\&=\text J\ \text s\tag{16}\end{align*}

となって角運動量の単位\(\text J \text s\)となるため、磁荷\(q_{\text m}\)と電荷\(q_{\text e}\)の量子化条件をプランク定数\(h\)を用いて

\begin{align*}\hat q_{\text m}\hat q_{\text e}=2nh \tag{17}\end{align*}

と表すことができる。

もし、E-B対応においても源場が磁束密度\(\boldsymbol B\)で力場が磁場\(\boldsymbol H\)であるなら単位ウェーバは

\begin{align*}\text {Wb}=\text A\ \text m\tag{18}\end{align*}

となり、電荷と磁荷で対称性が見辛くなる。また、量子化条件の式(17)もやや複雑になるが、実際には上記の式(18)のように磁荷を定義することもあり、そのような単位系をアンペア･メートル系と呼ぶ。

【前ページ】【次ページ】

HOME ＞電磁気学＞静磁場＞ E-H対応とE-B対応の等価性