HOME ＞ 電磁気学 ＞ 静磁場 ＞ 磁気モーメント
【前ページ】 【次ページ】
本ページでは…
本ページでは、磁気モーメント\(\boldsymbol m\)が
\begin{align*}\boldsymbol m=I\boldsymbol S\end{align*}
であることをみて、ループ電流のエネルギー\(U\)が
\begin{align*}U&=-\boldsymbol m\cdot\boldsymbol B\end{align*}
となり、ループ電流がつくる磁場\(\boldsymbol H\)が
\begin{align*}\boldsymbol H&=\frac{1}{4\pi\vert\boldsymbol r\vert^3}\ \left\{-\boldsymbol m+\frac{3(\boldsymbol r\cdot\boldsymbol m)\boldsymbol r}{\vert\boldsymbol r\vert^2} \right\}\end{align*}
となることを求める。
前ページまで…
前ページでは、アンペールの法則からビオ-サバールの法則
\begin{align*}d\boldsymbol H=\frac{I}{4\pi}\frac{d\boldsymbol l×\boldsymbol r}{\vert\boldsymbol r\vert^3}\end{align*}
を求めた。
内容
モーメント
｢位置ベクトル\(\boldsymbol r\)｣と｢位置\(\boldsymbol r\)における力\(\boldsymbol F\)や電荷\(q\)などの物理量｣の積(ベクトル同士の積なら外積)をモーメントといい、特に｢位置ベクトル\(\boldsymbol r\)｣と｢位置\(\boldsymbol r\)における力\(\boldsymbol F\)｣の外積であるモーメントを力のモーメント\(\boldsymbol N\)
\begin{align*}\boldsymbol N&=\boldsymbol r×\boldsymbol F\tag{1}\end{align*}
という。
磁気モーメント
いま、電流\(I\)が流れる半径\(a\)のループ電流が\(xy\)平面内に配置され、ループ電流の中心が原点にあって、右ネジの進む向きを\(z\)軸の正の向きとしたときに電流\(I\)の流れる向きを右ネジが進むときに回る向きとする。\(x\)軸の正の向きを基準として反時計回りでループ電流の面内角度を\(\varphi\)と定義すると、原点から微小長さ\(d\boldsymbol l\)への方向単位ベクトルは\(\boldsymbol e_\rho\)
\begin{align*}\boldsymbol e_\rho&=\begin{pmatrix}
\cos\varphi \\\sin\varphi\\0
\end{pmatrix}\end{align*}
、微小長さ\(d\boldsymbol l\)の向きを表す方向単位ベクトルは\(\boldsymbol e_\varphi\)
\begin{align*}\boldsymbol e_\varphi&=\begin{pmatrix}
-\sin\varphi \\\cos\varphi\\0
\end{pmatrix}\end{align*}
となる。そのため、微小長さ\(d\boldsymbol l\)の位置は\(a\boldsymbol e_\rho\)となり、微小長さ\(d\boldsymbol l\)は
\begin{align*}d\boldsymbol l&=a\sin(d\varphi)\boldsymbol e_\varphi\\&\simeq ad\varphi\boldsymbol e_\varphi\tag{2}\end{align*}
と表される。
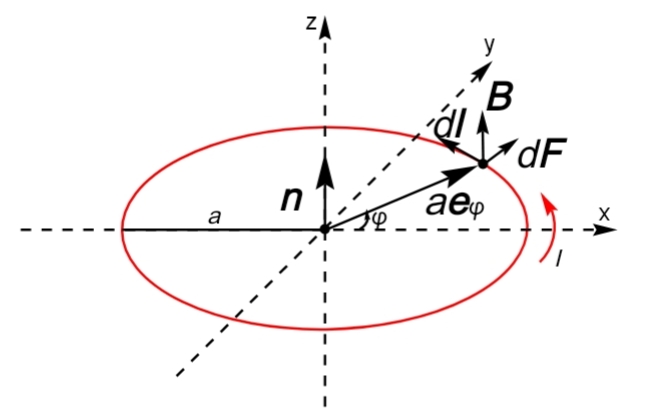磁束密度Bの下でのループ電流磁束密度\(\boldsymbol B\)の下で電流\(I\)が流れる微小長さ\(d\boldsymbol l\)が受ける力\(d\boldsymbol F\)は
\begin{align*}d\boldsymbol F&=Id\boldsymbol l×\boldsymbol B\\&=Iad\varphi\boldsymbol e_\varphi×\boldsymbol B\tag{3}\end{align*}
である(以前のページを参照)ため、微小長さ\(d\boldsymbol l\)における力のモーメント\(d\boldsymbol N\)は
\begin{align*}d\boldsymbol N&=Ia^2d\varphi(\boldsymbol e_\rho\cdot\boldsymbol B)\boldsymbol e_\varphi\tag{4}\end{align*}
\begin{align*}d\boldsymbol N&=a\boldsymbol e_\rho×d\boldsymbol F\\&=Ia^2d\varphi \boldsymbol e_\rho×(\boldsymbol e_\varphi×\boldsymbol B)\\&=Ia^2d\varphi\left\{(\boldsymbol e_\rho\cdot\boldsymbol B)\boldsymbol e_\varphi-(\boldsymbol e_\rho\cdot\boldsymbol e_\varphi)\boldsymbol B\right\}\\&=Ia^2d\varphi(\boldsymbol e_\rho\cdot\boldsymbol B)\boldsymbol e_\varphi\end{align*}
3行目への変形ではベクトル三重積の公式
\begin{align*}\boldsymbol a×(\boldsymbol b×\boldsymbol c)=(\boldsymbol a\cdot\boldsymbol c)\boldsymbol b-(\boldsymbol a\cdot\boldsymbol b)\boldsymbol c\end{align*}
を用い、4行目への変形ではベクトル\(\boldsymbol e_\rho\)とベクトル\(\boldsymbol e_\varphi\)が直角であることを用いた。
となる。また、ループ電流における力のモーメント\(\boldsymbol N\)は\(\varphi=0\)から\(\varphi=2\pi\)までの積分で表され
\begin{align*}\boldsymbol N&=-I\pi a^2(\boldsymbol e_\varphi×\boldsymbol e_\rho)×\boldsymbol B\tag{5}\end{align*}
\begin{align*}\boldsymbol N&=Ia^2\int^{2\pi}_0d\varphi\ (\boldsymbol e_\rho\cdot\boldsymbol B)\boldsymbol e_\varphi\\&=Ia^2\int^{2\pi}_0d\varphi\ (B_x\cos\varphi+B_y\sin\varphi)\begin{pmatrix}
-\sin\varphi \\\cos\varphi\\0
\end{pmatrix}\\&=Ia^2\int^{2\pi}_0d\varphi\ \begin{pmatrix}
-B_y\sin^2\varphi \\B_x\cos^2\varphi\\0
\end{pmatrix}\\&=I\pi a^2\begin{pmatrix}
-B_y \\B_x\\0
\end{pmatrix}\\&=-I\pi a^2(\boldsymbol e_\varphi×\boldsymbol e_\rho)×\boldsymbol B\end{align*}
2行目への変形では次の関係式
\begin{align*}\boldsymbol e_\rho&=\begin{pmatrix}
\cos\varphi \\\sin\varphi\\0
\end{pmatrix}\\\boldsymbol e_\varphi&=\begin{pmatrix}
-\sin\varphi \\\cos\varphi\\0
\end{pmatrix}\\\boldsymbol B&=\begin{pmatrix}
B_x \\B_y\\B_z
\end{pmatrix}\end{align*}
を用い、3行目への変形では次の関係式
\begin{align*}\int^{2\pi}_0d\varphi\
\sin\varphi\cos\varphi=\int^{2\pi}_0d\varphi\
\frac{\sin2\varphi}{2}=0\end{align*}
を用い、4行目への変形では次の関係式
\begin{align*}\int^{2\pi}_0d\varphi\
\sin^2\varphi&=\frac{1}{2}\int^{2\pi}_0d\varphi\
(1-\cos2\varphi)\\&=\pi\\\int^{2\pi}_0d\varphi\
\cos^2\varphi&=\frac{1}{2}\int^{2\pi}_0d\varphi\
(1+\cos2\varphi)\\&=\pi\end{align*}
を用い、5行目への変形では次の関係式
\begin{align*}\boldsymbol e_\varphi×\boldsymbol e_\rho=-\begin{pmatrix}
0\\
0\\1
\end{pmatrix}\end{align*}
用いた。
となる。ここで、ベクトル\(-\boldsymbol e_\varphi×\boldsymbol e_\rho\)
\begin{align*}-\boldsymbol e_\varphi×\boldsymbol e_\rho=\begin{pmatrix}
0\\
0\\1
\end{pmatrix}\end{align*}
は\(z\)軸の正の向きを向く方向単位ベクトルであり、電流\(I\)が流れる向きを右ネジが進むときに回る向きとしたときに右ネジの進む向きとなる。その向きを方向単位ベクトル\(\boldsymbol n\)
\begin{align*}\boldsymbol n=-\boldsymbol e_\varphi×\boldsymbol e_\rho\end{align*}
で表すと、大きさがループ電流のつくる面積\(S=\pi a^2\)で向きが面に垂直な\(\boldsymbol n\)である面積ベクトル\(\boldsymbol S=\pi a^2\boldsymbol n\)を定義できる。この面積ベクトル\(\boldsymbol S\)を用いると力のモーメント\(\boldsymbol N\)は
\begin{align*}\boldsymbol N&=I\boldsymbol S×\boldsymbol B\tag{6}\end{align*}
となる。ここで、ループ電流の力のモーメント\(\boldsymbol N\)に現れる\(I\boldsymbol S\)という量は｢ループ電流がつくる面積ベクトル\(\boldsymbol S\)｣と｢ループ電流を流れる電流の大きさ\(I\)｣との積となっているためこれもモーメントであり、磁気モーメントという。一般的に、磁気モーメントは記号\(\boldsymbol m\)を用いて
\begin{align*}\boldsymbol m=I\boldsymbol S\tag{7}\end{align*}
と表す。
磁気モーメント\(\boldsymbol m\)を用いて力のモーメント\(\boldsymbol N\)を表すと
\begin{align*}\boldsymbol N=\boldsymbol m×\boldsymbol B\tag{8}\end{align*}
となり、磁気モーメント\(\boldsymbol m\)が磁束密度\(\boldsymbol B\)に平行であるならば力のモーメント\(\boldsymbol N\)は\(\boldsymbol 0\)となり、ループ電流は\(\boldsymbol S\)方向または\(-\boldsymbol S\)方向に沿って動くだけである。しかし、 磁気モーメント\(\boldsymbol m\)が磁束密度\(\boldsymbol B\)に平行でなければ力のモーメント\(\boldsymbol N\)は \(\boldsymbol 0\)にはならず、ループ電流の各点において力\(\boldsymbol F\)は磁気モーメント\(\boldsymbol m\)に平行な成分を持ち、ループ電流は回転する。
ループ電流の磁場
小さいループ電流が作る磁場\(\boldsymbol H\)はビオ-サバールの法則から求めることができる。
微小長さ\(d\boldsymbol l\)の位置からベクトル\(\boldsymbol r’\)の位置に作られる磁場は
\begin{align*}d\boldsymbol H=\frac{I}{4\pi}\frac{d\boldsymbol l×\boldsymbol r’}{\vert\boldsymbol r’\vert^3}\tag{9}\end{align*}
と表される(前ページを参照)から、微小長さの電流が原点からベクトル\(\boldsymbol r\)の位置に作る磁場は
\begin{align*}d\boldsymbol H&=\frac{Iad\varphi}{4\pi\vert\boldsymbol r\vert^3}\left\{\boldsymbol e_\varphi×\boldsymbol r\left(1+\frac{3(\boldsymbol r\cdot a\boldsymbol e_\rho)}{\vert\boldsymbol r\vert^2}\right)-a\boldsymbol e_\varphi×\boldsymbol e_\rho\right\}\tag{10}\end{align*}
\begin{align*}d\boldsymbol H&=\frac{I}{4\pi}\frac{a d\varphi \boldsymbol e_\varphi×\boldsymbol r’}{\vert\boldsymbol r’\vert^3}\\&=\frac{I}{4\pi}\frac{a d\varphi \boldsymbol e_\varphi×(\boldsymbol r-a\boldsymbol e_\rho)}{\vert\boldsymbol r-a\boldsymbol e_\rho\vert^3}\\&=\frac{Iad\varphi}{4\pi} \boldsymbol e_\varphi×\left(\frac{(\boldsymbol r-a\boldsymbol e_\rho)}{\vert\boldsymbol r\vert^3}+\frac{3(\boldsymbol r\cdot a\boldsymbol e_\rho)\boldsymbol r}{\vert\boldsymbol r\vert^5}\right)\\&=\frac{Iad\varphi}{4\pi\vert\boldsymbol r\vert^3}\left\{\boldsymbol e_\varphi×\boldsymbol r\left(1+\frac{3(\boldsymbol r\cdot a\boldsymbol e_\rho)}{\vert\boldsymbol r\vert^2}\right)-a\boldsymbol e_\varphi×\boldsymbol e_\rho\right\}\end{align*}
1行目では
\begin{align*}\boldsymbol r’=\boldsymbol r-a\boldsymbol e_\rho\end{align*}
の関係を使い、2行目への変形では\(a\boldsymbol e_\rho\)が十分小さいため、\(\boldsymbol d\)が十分小さいときに成り立つ次式を用いた(以前のページを参照)。
\begin{align*}\frac{\boldsymbol r-\boldsymbol d}{\vert\boldsymbol r-\boldsymbol d\vert^3}\simeq\frac{\boldsymbol r-\boldsymbol d}{\vert\boldsymbol r\vert^3}+\frac{3(\boldsymbol r\cdot\boldsymbol d)\boldsymbol r}{\vert\boldsymbol r\vert^5}\tag{10}\end{align*}
となる。
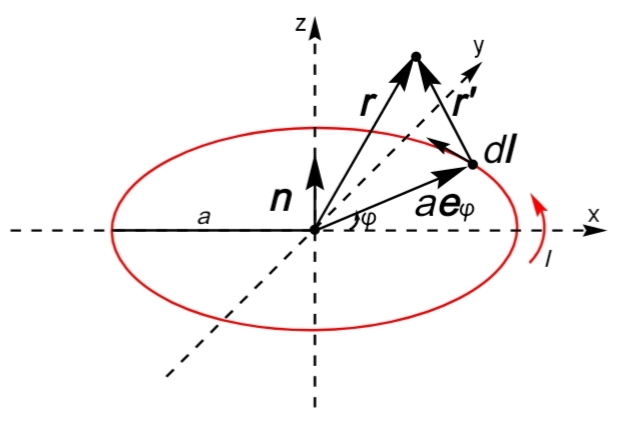ループ電流がつくる磁場Hそして、ループ電流が作る磁場は式(10)を次のように\(\varphi=0\)から\(\varphi=2\pi\)まで積分すれば良い。
\begin{align*}\boldsymbol H&=\frac{Ia}{4\pi\vert\boldsymbol r\vert^3}\int^{2\pi}_0d\varphi\ \left\{\boldsymbol e_\varphi×\boldsymbol r\left(1+\frac{3(\boldsymbol r\cdot a\boldsymbol e_\rho)}{\vert\boldsymbol r\vert^2}\right)-a\boldsymbol e_\varphi×\boldsymbol e_\rho\right\}\tag{11}\end{align*}
ここで、ベクトル\(\boldsymbol e_\varphi\)とベクトル\(\boldsymbol r\)は
\begin{align*}\boldsymbol e_\varphi&=\begin{pmatrix}
-\sin\varphi \\\cos\varphi\\0
\end{pmatrix}\\\boldsymbol r&=\begin{pmatrix}
x\\y\\z
\end{pmatrix}\end{align*}
であるから、次の関係
\begin{align*}\int^{2\pi}_0d\varphi\ \boldsymbol e_\varphi×\boldsymbol r&=\int^{2\pi}_0d\varphi\ \begin{pmatrix}
z\cos\varphi\\z\sin\varphi\\-y\sin\varphi-y\cos\varphi
\end{pmatrix}\\&=0\tag{12}\end{align*}
2行目への変形では
\begin{align*}\int^{2\pi}_0d\varphi\
\sin\varphi=\int^{2\pi}_0d\varphi\
\cos\varphi=0\end{align*}
を用いた。
が成り立ち、式(11)は少しシンプルになる。
\begin{align*}\boldsymbol H&=\frac{Ia^2}{4\pi\vert\boldsymbol r\vert^3}\int^{2\pi}_0d\varphi\ \left\{\boldsymbol e_\varphi×\boldsymbol r\left(\frac{3(\boldsymbol r\cdot \boldsymbol e_\rho)}{\vert\boldsymbol r\vert^2}\right)-\boldsymbol e_\varphi×\boldsymbol e_\rho\right\}\tag{13}\end{align*}
次に、式(13)に現れる量
\begin{align*}\int^{2\pi}_0d\varphi\ (\boldsymbol r\cdot \boldsymbol e_\rho)\boldsymbol e_\varphi×\boldsymbol r\end{align*}
\begin{align*}\int^{2\pi}_0d\varphi\ \boldsymbol e_\varphi×\boldsymbol e_\rho\end{align*}
を計算すると
\begin{align*}\int^{2\pi}_0d\varphi\ (\boldsymbol r\cdot \boldsymbol e_\rho)\boldsymbol e_\varphi×\boldsymbol r=\pi z\boldsymbol r+\pi\vert \boldsymbol r\vert^2\boldsymbol e_\varphi×\boldsymbol e_\rho\tag{14}\end{align*}
\begin{align*}\int^{2\pi}_0d\varphi\ (\boldsymbol r\cdot \boldsymbol e_\rho)\boldsymbol e_\varphi×\boldsymbol r&=\int^{2\pi}_0d\varphi\ (x\cos\varphi+y\sin\varphi)\begin{pmatrix}
z\cos\varphi \\
z\sin\varphi \\ -y\sin\varphi-x\cos\varphi
\end{pmatrix}\\&=\int^{2\pi}_0d\varphi\ \begin{pmatrix}
xz\cos^2\varphi \\
yz\sin^2\varphi \\ -x^2\cos^2\varphi-y^2\sin^2\varphi
\end{pmatrix}\\&=\pi\begin{pmatrix}
xz\\
yz\\ z^2-\vert\boldsymbol r\vert^2
\end{pmatrix}\\&=\pi z\begin{pmatrix}
x\\
y\\ z
\end{pmatrix}-\pi\begin{pmatrix}
0\\
0\\ \vert\boldsymbol r\vert^2
\end{pmatrix}\\&=\pi z\boldsymbol r+\pi\vert \boldsymbol r\vert^2\boldsymbol e_\varphi×\boldsymbol e_\rho\end{align*}
1行目では次のベクトル
\begin{align*}\boldsymbol e_\rho&=\begin{pmatrix}
\cos\varphi \\\sin\varphi\\0
\end{pmatrix}\\\boldsymbol e_\varphi&=\begin{pmatrix}
-\sin\varphi \\\cos\varphi\\0
\end{pmatrix}\\\boldsymbol r&=\begin{pmatrix}
x\\y\\z
\end{pmatrix}\end{align*}
の内積と外積を用い、2行目への変形では次の関係式
\begin{align*}\int^{2\pi}_0d\varphi\
\sin\varphi\cos\varphi=\int^{2\pi}_0d\varphi\
\frac{\sin2\varphi}{2}=0\end{align*}
を用い、3行目への変形では次の関係式
\begin{align*}\int^{2\pi}_0d\varphi\
\sin^2\varphi&=\frac{1}{2}\int^{2\pi}_0d\varphi\
(1-\cos2\varphi)\\&=\pi\\\int^{2\pi}_0d\varphi\
\cos^2\varphi&=\frac{1}{2}\int^{2\pi}_0d\varphi\
(1+\cos2\varphi)\\&=\pi\end{align*}
を用い、6行目への変形では次の関係式
\begin{align*}\boldsymbol e_\varphi×\boldsymbol e_\rho=-\begin{pmatrix}
0\\
0\\1
\end{pmatrix}\end{align*}
を用いた。
\begin{align*}\int^{2\pi}_0d\varphi\ \boldsymbol e_\varphi×\boldsymbol e_\rho=2\pi(\boldsymbol e_\varphi×\boldsymbol e_\rho)\tag{15}\end{align*}
\begin{align*}\int^{2\pi}_0d\varphi\ \boldsymbol e_\varphi×\boldsymbol e_\rho&=\boldsymbol e_\varphi×\boldsymbol e_\rho\int^{2\pi}_0d\varphi\ \\&=2\pi(\boldsymbol e_\varphi×\boldsymbol e_\rho)\end{align*}
2行目への変形では次の外積が定数であること
\begin{align*}\boldsymbol e_\varphi×\boldsymbol e_\rho=\begin{pmatrix}
0\\
0\\1
\end{pmatrix}\end{align*}
を用いた。
となるため、式(13)に代入すると
\begin{align*}\boldsymbol H&=\frac{I\pi a^2}{4\pi\vert\boldsymbol r\vert^3}\ \left\{\boldsymbol e_\varphi×\boldsymbol e_\rho-\frac{3}{\vert\boldsymbol r\vert^2} (\boldsymbol r\cdot(\boldsymbol e_\varphi×\boldsymbol e_\rho))\boldsymbol r\right\}\tag{16}\end{align*}
\begin{align*}H&=\frac{Ia^2}{4\pi\vert\boldsymbol r\vert^3}\ \left\{\frac{3}{\vert\boldsymbol r\vert^2}(\pi z\boldsymbol r+\pi\vert\boldsymbol r\vert^2\boldsymbol e_\varphi×\boldsymbol e_\rho)-2\pi\boldsymbol e_\varphi×\boldsymbol e_\rho\right\}\\&=\frac{I\pi a^2}{4\pi\vert\boldsymbol r\vert^3}\ \left\{\frac{3}{\vert\boldsymbol r\vert^2} z\boldsymbol r+\boldsymbol e_\varphi×\boldsymbol e_\rho\right\}\\&=\frac{I\pi a^2}{4\pi\vert\boldsymbol r\vert^3}\ \left\{-\frac{3}{\vert\boldsymbol r\vert^2} (\boldsymbol r\cdot(\boldsymbol e_\varphi×\boldsymbol e_\rho))\boldsymbol r+\boldsymbol e_\varphi×\boldsymbol e_\rho\right\}\end{align*}
3行目への変形では次の関係式
\begin{align*}\boldsymbol r&=\begin{pmatrix}
x\\y\\z
\end{pmatrix}\boldsymbol e_\varphi×\boldsymbol e_\rho&=\begin{pmatrix}
0\\
0\\1
\end{pmatrix}\end{align*}
を用いた。
最後に磁気モーメント\(\boldsymbol m\)で表すと次のようになり、ループ電流がつくる磁場\(\boldsymbol H\)が得られる。
\begin{align*}\boldsymbol H&=\frac{1}{4\pi\vert\boldsymbol r\vert^3}\ \left\{-\boldsymbol m+\frac{3(\boldsymbol r\cdot\boldsymbol m)\boldsymbol r}{\vert\boldsymbol r\vert^2} \right\}\tag{17}\end{align*}
\begin{align*}\boldsymbol H&=\frac{I\pi a^2}{4\pi\vert\boldsymbol r\vert^3}\ \left\{-\boldsymbol n+\frac{3(\boldsymbol r\cdot\boldsymbol n)\boldsymbol r}{\vert\boldsymbol r\vert^2} \right\}\\&=\frac{I}{4\pi\vert\boldsymbol r\vert^3}\ \left\{-\boldsymbol S+\frac{3(\boldsymbol r\cdot\boldsymbol S)\boldsymbol r}{\vert\boldsymbol r\vert^2} \right\}\\&=\frac{1}{4\pi\vert\boldsymbol r\vert^3}\ \left\{-\boldsymbol m+\frac{3(\boldsymbol r\cdot\boldsymbol m)\boldsymbol r}{\vert\boldsymbol r\vert^2} \right\}\end{align*}
1行目の変形では次の関係式
\begin{align*}\boldsymbol n=-\boldsymbol e_\varphi×\boldsymbol e_\rho\end{align*}
を用い、2行目への変形では
\begin{align*}\boldsymbol S=\pi a^2\boldsymbol n\end{align*}
を用い、3行目への変形では
\begin{align*}\boldsymbol m=I\boldsymbol S\end{align*}
を用いた。
磁気モーメントと磁化
以前のページで、磁性体に自由電流が近づいたとき、電子のスピンや角運動量(小さなループ電流)が整列し、磁性体表面に磁化電流が現れることをみた。また、別のページでは、自由電流が磁場\(\boldsymbol B\)を作ったように磁化電流は磁化\(\boldsymbol M\)を作ることをみたため、磁気モーメント\(\boldsymbol m\)と磁化\(\boldsymbol M\)にはある関係が成り立つ。
磁化\(\boldsymbol M\)の単位は磁場\(\boldsymbol H\)の単位と同様に\(\text A\cdot\text m^{-1}\)であるため、磁化\(\boldsymbol M\)は磁気力線と同じ単位\(\text A\cdot \text m\)を持つ仮想的な線の面密度である(磁気力線は自由電流から生じるもののため、磁化電流から生じる今回のような線はあえて｢仮想的な線｣と表現した)。また、磁気モーメント\(\boldsymbol m\)の単位は\(\text A\cdot \text m^2\)であり、磁気力線と同じ単位\(\text A\cdot \text m\)を持つ仮想的な線の本数に長さを掛けたものである。よって、体積\(\Delta V\)中に磁気モーメントが\(\boldsymbol m_{i}\)であるループ電流が\(n\)個存在するとき、単位体積あたりの磁気モーメントの和が磁化\(\boldsymbol M\)である。
\begin{align*}\boldsymbol M=\frac{\sum_{i=1}^n\boldsymbol m_i}{\Delta V}\tag{18}\end{align*}
磁気モーメントと磁気双極子モーメント
小さいループ電流がつくる磁場\(\boldsymbol H\)は
\begin{align*}\boldsymbol H&=\frac{1}{4\pi\vert\boldsymbol r\vert^3}\ \left\{-\boldsymbol m+\frac{3(\boldsymbol r\cdot\boldsymbol m)\boldsymbol r}{\vert\boldsymbol r\vert^2} \right\}\tag{17}\end{align*}
であり、磁気双極子がつくる磁場\(\boldsymbol H\)は
\begin{align*}\boldsymbol H&=\frac{1}{4\pi\mu_0\vert\boldsymbol r\vert^3}\left(-\boldsymbol p_{\text m}+\frac{3(\boldsymbol r\cdot\boldsymbol p_{\text m})\boldsymbol r}{\vert\boldsymbol r\vert^2}\right)\tag{19}\end{align*}
である(以前のページを参照、注意としてこの式が成り立つのは磁性体が存在しない場合だけである)。そのため、磁気モーメント\(\boldsymbol m\)と磁気双極子モーメント\(\boldsymbol p_{\text m}\)とに次の関係
\begin{align*}\boldsymbol m=\frac{1}{\mu_0}\boldsymbol p_{\text m}\tag{19}\end{align*}
があれば小さいループ電流がつくる磁場\(\boldsymbol H\)と磁気双極子がつくる磁場\(\boldsymbol H\)は等しくなる。この式(19)を変形すると
\begin{align*}q_{\text m}\boldsymbol d=\frac{1}{\mu_0}I\pi a^2\boldsymbol n\tag{20}\end{align*}
となり、ベクトル\(\boldsymbol d\)とベクトル\(\boldsymbol n\)が同方向を向いていると仮定すると、式(20)両辺のベクトルの大きさは
\begin{align*}q_{\text m}=\frac{I\pi a^2}{\mu_0\vert\boldsymbol d\vert}\tag{21}\end{align*}
となる(\(\boldsymbol n\)は方向単位ベクトルであることに注意する)。
つまり、小さいループ電流が｢距離が\(\vert\boldsymbol d\vert\)で磁荷の大きさが式(21)であり、面積ベクトルの向きを向いている磁気双極子｣と等価であると考えたとき、それぞれがつくる磁場\(\boldsymbol H\)は一致する(再度、注意だが、この式が成り立つのは磁性体が存在しない場合だけである)。
ループ電流が受ける力のモーメント\(\boldsymbol N\)は
\begin{align*}\boldsymbol N=\boldsymbol m×\boldsymbol B\tag{8}\end{align*}
であり、磁気双極子モーメントが受ける力のモーメント\(\boldsymbol N\)は
\begin{align*}\boldsymbol N=\boldsymbol p_{\text m}×\boldsymbol H\tag{22}\end{align*}
であった。磁性体が存在しないとき、次の関係
\begin{align*}\boldsymbol B=\mu_0\boldsymbol H\tag{23}\end{align*}
が成り立つため、式(8)は
\begin{align*}\boldsymbol N=\boldsymbol m×\mu_0\boldsymbol H\tag{24}\end{align*}
となり、式(19)
\begin{align*}\boldsymbol m=\frac{1}{\mu_0}\boldsymbol p_{\text m}\tag{19}\end{align*}
を考慮すると式(22)と式(24)は等しい。つまり、ループ電流が受ける力のモーメント\(\boldsymbol N\)と磁気双極子が受けるモーメント式\(\boldsymbol N\)は等しい。
ループ電流のエネルギー
磁場\(\boldsymbol H\)の下に置かれている磁気双極子のエネルギーは
\begin{align*}U&=\boldsymbol p_{\text m}\cdot\boldsymbol H\tag{25}\end{align*}
であったため、式(19)と式(23)を代入すると磁束密度\(\boldsymbol B\)の下に置かれているループ電流のエネルギーは
\begin{align*}U&=\boldsymbol m\cdot\boldsymbol B\tag{25}\end{align*}
となり、どちらのエネルギーもモーメントと力場の内積となっている。
次ページから…
次ページでは、E-B対応において、静電場と静磁場の類似点も相違点について述べる。
【前ページ】 【次ページ】
HOME ＞ 電磁気学 ＞ 静磁場 ＞ 磁気モーメント
